---

Digging for Roots

By: John Vereen

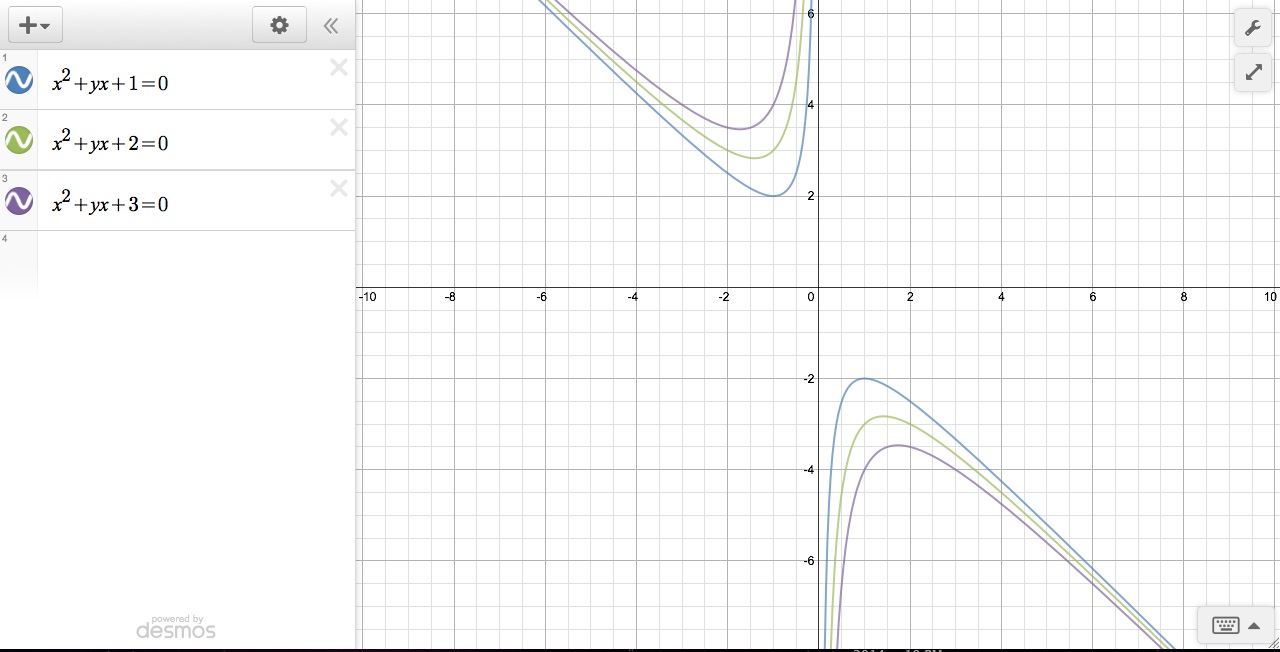
Let’s explore some different types of quadratic functions. We are going to first explore function of the form x²+bx+1=0. However, we will be exploring these functions in the x-b plane instead of the x-y plane. We will see how a varying c value affects the shape of each graph on the x-b plane. As we can see above, the graphs have asymptotes at the b-axis and at x=-b. Also, as |c| increases, the parabolas move further away from the x-axis because the roots are becoming larger.

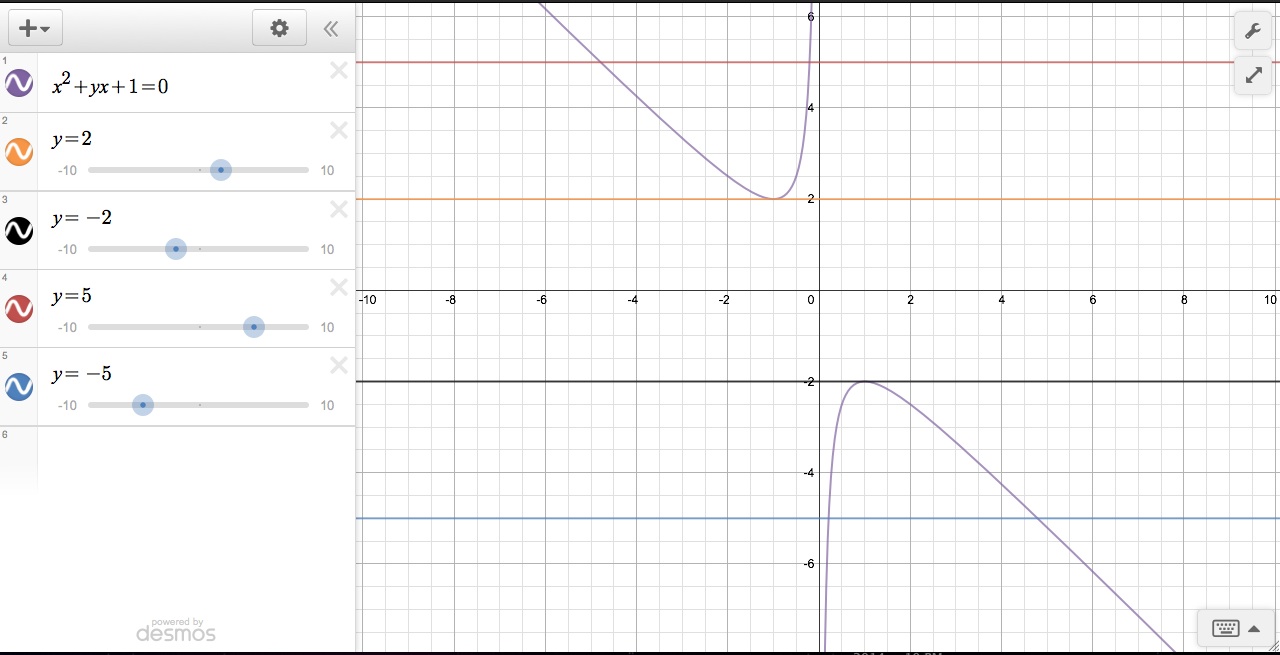
We have interesting results for the roots of equations of the form x²+bx+1=0 when we set b equal to certain real values. There is actually a method to finding roots that is non-algebraic and does not require the quadratic formula. If we use a graph and draw a horizontal line at a specific value for b, such as b=2, we will then we will see what values we have for b for the equation. There are three noteworthy findings from the picture above.

1) When |b|<2, there is no real solution.

2) When |b|=2, there is exactly one real solution.

3) When |b|>2, there are two real solutions.

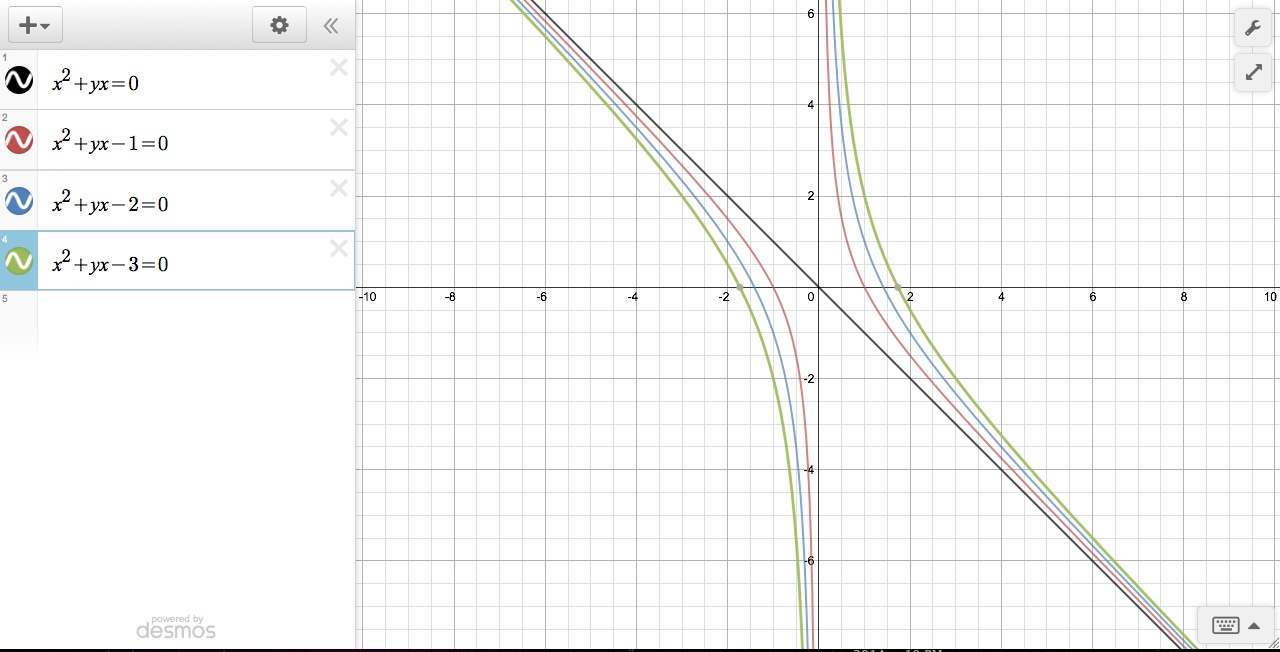
When we change the graph from x²+bx+1=0 to x²+bx-1=0. We see some striking differences in the two graphs. Instead of the solution sets being on the interior of v-like shapes of the asymptotes created by the b-axis and x=-b, the solution sets are on the exterior. It also appears that there are always 2 solutions for b = the set of real numbers instead of 0, 1, or 2 solutions.

So, what have we learned about the set of solutions for x²+bx+1=0 and x²+bx-1=0. Well, if we have the equation x²+bx+1=0, then we have the possibility of 0, 1, or 2 real solutions. When |b|<2, there are no real solutions. When |b|=2, there is exactly one real solution. When |b|>2, then there are exactly two real solutions. Also, when we have x²+bx-1=0, then there are always 2 real solutions to the equation.